Introduction

Kohonon's SOMs are a type of unsupervised learning. The goal is to discover some underlying structure of the data. However, the kind of structure we are looking for is very different than, say, PCA or vector quantization.

Kohonen's SOM is called a topology-preserving map because there is a topological structure imposed on the nodes in the network. A topological map is simply a mapping that preserves neighborhood relations.

In the nets we have studied so far, we have ignored the geometrical arrangements of output nodes. Each node in a given layer has been identical in that each is connected with all of the nodes in the upper and/or lower layer. We are now going to take into consideration that physical arrangement of these nodes. Nodes that are "close" together are going to interact differently than nodes that are "far" apart.

What do we mean by "close" and "far"? We can think of organizing the output nodes in a line or in a planar configuration.

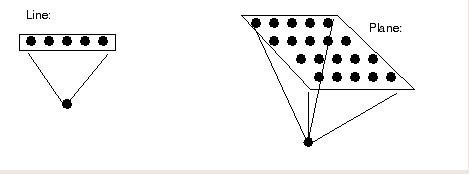
The goal is to train the net so that nearby outputs correspond to nearby inputs.

E.g. if x1 and x2 are two input vectors and t1 and t2 are the locations of the corresponding winning output nodes, then t1 and t2 should be close if x1 and x2 are similar. A network that performs this kind of mapping is called a feature map.

In the brain, neurons tend to cluster in groups. The connections within the group are much greater than the connections with the neurons outside of the group. Kohonen's network tries to mimick this in a simple way.